On a vu à la section précédente (4.1.1) que les méthodes de datation relatives, principalement par les fossiles, n'ont pas permis d'obtenir une idée du temps géologique réel. Non seulement ne connaissions-nous pas l'âge des diverses couches géologiques, mais on ne connaissait même pas l'âge de la Terre.
 | L'âge de la Terre |
Il fallut attendre la découverte de la radioactivité par Marie et Pierre Curie, au début du 20e siècle, pour avoir enfin cet outil qui permit de se faire une idée réaliste du temps géologique, c'est-à-dire obtenir des âges géologiques absolus, et de déterminer l'âge vénérable de notre planète.
Cet outil, la datation radiométrique, utilise certains éléments chimiques qui ont la propriété de se désintégrer radioactivement. En calculant le temps qu'a mis une certaine portion d'un élément contenu dans un minéral à se désintégrer, on obtient l'âge de formation de ce minéral.
Qu'est-ce que la radioactivité?
Comme on l'a vu à la section 2, l'atome est composé d'un noyau (protons + neutrons) autour duquel gravitent les électrons. Toute la masse de l'atome est concentrée dans le noyau, les électrons ayant une masse négligeable.
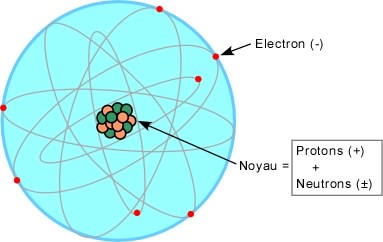
Par définition:
masse atomique = noyau = nombre de protons (+) + nombre de neutrons (±)
numéro atomique = nombre de protons (+)
La radioactivité est due à l'instabilité du noyau qui se désintègre par émission d'énergie, principalement sous deux formes:
d'où une perte de 4 dans la masse atomique et une perte de 2 dans le numéro atomique;
cet électron vient du noyau; il faut donc aller le chercher chez un neutron (±) qui alors devient un proton (+). Il y a donc gain d'un proton, d'où un gain de 1 au numéro atomique, mais aucun changement de masse atomique, car l'électron a une masse négligeable.
Un exemple : la désintégration de l'uranium 238 (238U) en plomb 206 (206Pb)
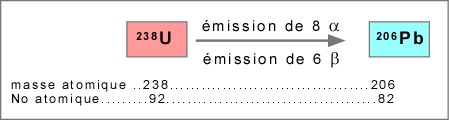
L'émission de 8 a entraîne la perte de 8 x (2 protons + 2 neutrons), ce qui signifie une perte de 32 à la masse atomique, ainsi que la perte de 8 x 2 protons qui signifie une perte de 16 au numéro atomique.
L'émission de 6 b entraîne la perte de 6 électrons, donc pas de changement à la masse atomique, mais un gain de 6 au numéro atomique.
Le bilan des gains et pertes s'établit donc ainsi:
numéro atomique: 92 - 16 + 6 = 82 (numéro atomique du Pb)
La désintégration se fait par étapes successives, selon la suite:
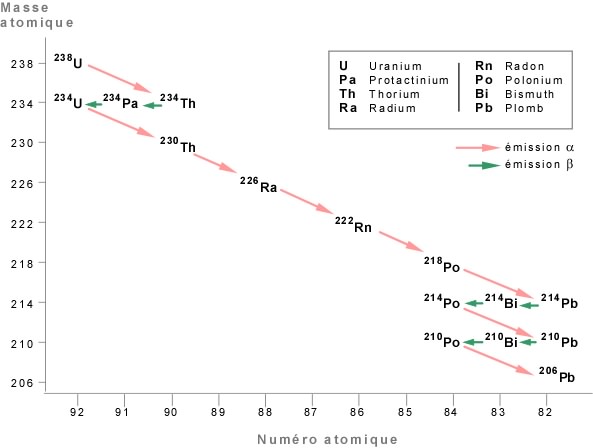
La Datation radiométrique
La réaction de désintégration peut se résumer ainsi: un élément parent (l'uranium dans l'exemple ci-haut) se transforme progressivement en un élément rejeton (ici le plomb). Cette désintégration met un certain temps à se faire; c'est ce paramètre temps qui nous intéresse.

Ici, le temps est le temps total pour que tout l'élément parent soit transformé en élément rejeton.
On peut illustrer ainsi la progression de la désintégration :
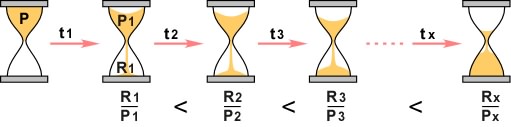
Après un temps 1 (t1), une partie de la quantité originelle d'élément parent (P) aura été transformée en une quantité R1 d'élément rejeton; il ne restera qu'une quantité P1 de l'élément parent, ce qui peut s'exprimer par le rapport R1 sur P1. Après un temps 2 (t2), on obtiendra un rapport R2 sur P2, plus grand que le précédent, ... et ainsi de suite.
La valeur du rapport R sur P est donc fonction du temps de désintégration. Le taux de désintégration est différent d'un type de désintégration à l'autre, mais toujours le même pour une désintégration donnée. Comme on connaît bien les constantes de désintégration pour les diverses réactions qu'on utilise couramment, on est capable de calculer le temps de désintégration pour une valeur donnée du rapport R sur P, à l'aide de ces constantes. Ce qu'on calcule, c'est le temps qu'a mis la désintégration à se rendre à cette proportion entre rejeton et parent. Voilà un point très important en ce qui concerne les datations radiométriques: ce qu'on détermine, c'est depuis combien de temps la désintégration a lieu ou, si on préfère, depuis combien de temps a commencé la désintégration.
En pratique, il s'agit d'utiliser des minéraux qui contiennent des éléments radioactifs, comme par exemple le zircon, un silicate de zirconium (ZrSiO4). Dans ce minéral, une certaine quantité du zirconium peut être substituée par l'uranium, soit (U,Zr)SiO4, ce qui rend le minéral utile pour les datations. Au moment où le minéral cristallise, il incorpore une certaine quantité d'uranium, mais pas de plomb. L'uranium va commencer, à ce moment, à se désintégrer radioactivement. En déterminant le rapport plomb sur uranium (rejeton/parent) par analyse en spectrométrie de masse dans un zircon donné, lequel zircon se trouve par exemple dans un granite, on peut calculer depuis combien de temps se fait la désintégration ou, en d'autres termes, il y a combien de temps qu'a cristallisé le zircon. Comme il a cristallisé en même temps que le granite qui le contient, c'est en ce sens qu'on obtient l'âge du granite, c'est-à-dire le moment de sa formation. C'est pourquoi, on parle d'âge radiométrique, c'est-à-dire un âge obtenu par la mesure des produits de la radioactivité.
Dans le cas de notre sablier, la courbe d'écoulement du sable s'exprime par une droite, une relation linéaire,représentée sur le graphique ci-dessous, où sont mis en relation, le pourcentage de l'élément parent et le temps exprimé en minutes.
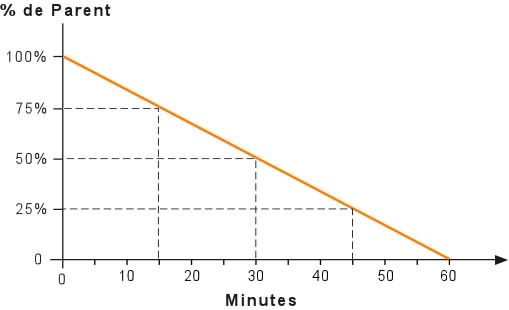
Supposons qu'il s'agisse d'un sablier d'une heure. Après un quart d'heure, le quart du volume de sable se sera écoulé et il restera 75% du sable dans la partie supérieure du sablier. Après une demie heure, il en restera 50%, et après trois quarts d'heure, il n'en restera que 25%.
Dans le cas de la radioactivité, la réaction de désintégration n'est pas linéaire, mais exponentielle: elle s'exprime par la courbe ci-dessous qui montre que le taux de désintégration diminue avec le temps. Le taux de désintégration est très rapide au début, et décroît par la suite.
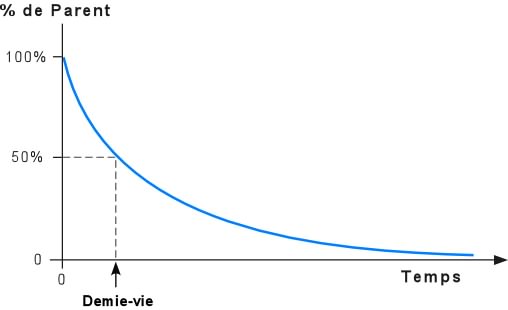
Des mesures en laboratoire ont montré que la désintégration suit une règle simple : la moitié des atomes parents qui se trouvent dans un système fermé se désintègre pour former des atomes rejetons dans un intervalle de temps fixe. Cet intervalle s'appelle la demie-vie. En clair, la demie-vie, c'est le temps nécessaire pour que la moitié de l'élément parent soit désintégrée. Attention, ce n'est pas la moitié de la vie de la désintégration, c'est le temps nécessaire pour que la moitié de l'élément parent soit désintégrée.
Voici une illustration qui permet de mieux visualiser ce qu'on entend par demie-vie. Prenons la réaction Uranium 238 - plomb 206 qui a une demie-vie de 4,5 Ga.
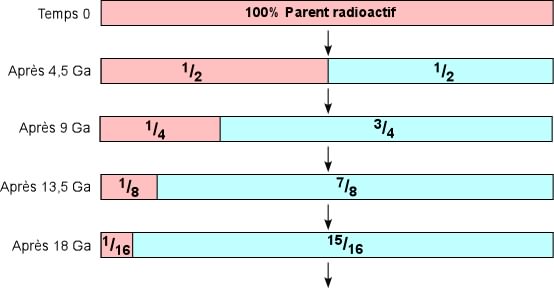
Après une demie-vie, i.e. 4,5 Ga, il restera la moitié de l'élément parent. Après un autre 4,5 Ga, soit au total 9 Ga, la moitié de ce qui restait sera désintégré, il restera donc le quart de l'élément parent. Et ainsi de suite.
Cela va s'exprimer de la façon suivante sur notre courbe de désintégration. Sur l'axe horizontal, le nombre de demies-vies, chacune de longueur égale. On voit bien que progressivement, les quantités d'élément parent diminuent à chaque demie-vie.
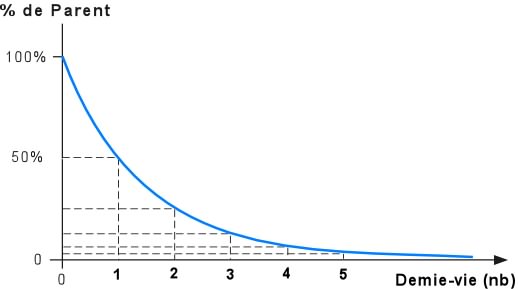
Voici quelques unes des désintégrations utilisées le plus couramment.:

Et le fameux Carbone-14?
A chaque fois qu'il est question de datation de roches ou d'autres matériaux anciens, on invoque inévitablement l'incontournable Carbone-14 (14C). Le 14C est en effet une méthode très utile pour la datation de certains matériaux géologiques, et particulièrement de matériaux archéologiques.
La méthode utilise la réaction de désintégration du carbone-14 en azote-14. Il faut savoir que le carbone commun dans la nature a une masse atomique de 12 (12C). Il se combine à l'oxygène atmosphérique (O2) pour former du CO2 dans lequel le carbone a une masse atomique de 12, soit le 12CO2. Mais en plus du 12C, il y a aussi, en bien plus faible quantité, du carbone de masse 13 (13C) et du carbone de masse 14 (14C); ces trois formes, de masse atomique différente pour un même élément, sont ce qu'on appelle des isotopes. Le 12C et le 13C sont des isotopes stables, c'est-à-dire qu'ils ne sont pas radioactifs, tandis que le 14C est un isotope radioactif; c'est lui qu'on utilise pour les datations.
Pour bien comprendre la méthode, il nous faut voir d'où vient le 14C et comment ce 14C est fixé, avec du 12C, par les organismes vivants, végétaux et animaux.
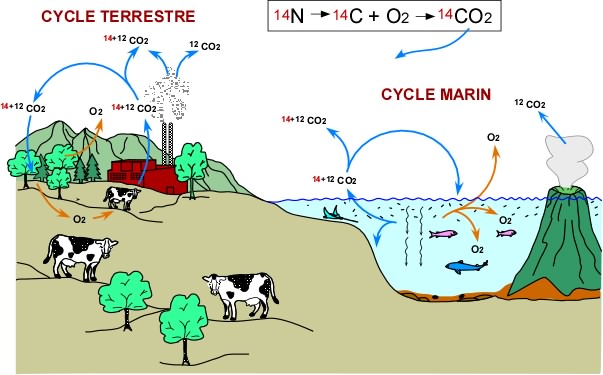
Le bombardement des gaz de la haute atmosphère par les rayons cosmiques fait que l'azote, de masse atomique 14 (14N) se transforme en 14C qui se combine à l'oxygène libre (O2) pour former du CO2, mais un CO2 particulier où le carbone est de masse atomique 14, soit le 14CO2. Ce 14CO2 se mélange au CO2 qui vient des autres sources, comme des volcans et de l'oxydation des matières organiques ou, aujourd'hui, de la combustion des hydrocarbures. Le CO2 qui provient du cycle photosynthèse-oxydation des matières organiques est aussi particulier. En effet, la photosynthèse consomme du CO2 atmosphérique, c'est-à-dire un CO2 qui contient en partie du 12C et en partie du 14C. C'est donc dire que la matière organique des végétaux et des animaux (qui consomment les végétaux) contiendra une certaine quantité de 14C. C'est ce 14C qui est utilisé pour les datations
Au départ donc, toute matière organique vivante (végétaux ou animaux) contient du 12C et du 14C (ainsi qu'une faible quantité de 13C). La proportion entre 14C et 12C dans les tissus organiques et le squelette métabolisés par l'organisme demeure la même tout au long de la vie de l'organisme, un rapport correspondant à celui qui se trouve dans le CO2 atmosphérique. En pratique, on peut donc dire que l'horloge démarre avec la mort de l'organisme; la proportion commence alors à changer à cause de la désintégration du 14C et du fait que le 12C demeure stable. Le produit de la désintégration du 14C, l'azote 14, est un gaz qui s'échappe dans la nature. En pratique, puisque le 12C est stable, on mesure le rapport entre, 14C et 12C. Connaissant le rapport qui existe dans la nature entre 14C et 12C, ainsi que la constante de désintégration, on peut comme dans les autres méthodes, calculer le temps qui s'est écoulé depuis la mort de l'organisme qui a fixé le carbone dans ses tissus ou son squelette. Par conséquent, l'âge que l'on obtient avec la méthode du 14C, c'est l'âge de la mort de l'organisme (du bois, des coquillages, de la tourbe, des tissus de lin, cotton, laine, etc...).
Mais la proportion 14C/12C est-elle vraiment demeurée constante à travers les temps géologiques?
Dans la méthode de datation par 14C, on prend pour acquis que la proportion 14C/12C n'a pas changé avec le temps géologique, ... ce qui n'est pas vrai. En effet, on sait aujourd'hui que cette proportion a varié avec le temps. On le sait par exemple en comparant l'âge obtenu à partir du 14C et l'âge obtenu en comptant les anneaux des arbres (dendrochronologie) ou les cernes de croissance de coraux, ou encore les varves (dépôts saisonniers) dans les lacs. On sait que la production de 14C a été variable, et généralement plus élevée dans le passé, ce qui implique que les âges non étalonnés en années dendrochronologiques (solaires) sont en réalité souvent plus jeunes que ce qu'ils paraissent d'après la chronologie 14C et ce, de manière non linéaire. C'est pourquoi il faut étalonner les dates 14C, procédure qu'on appelle aussi calibration. Ainsi, une date 14C de 5000 ans correspond-t-elle en réalité à environ 5720 années solaires, tandis qu'une date 14C de 10 000 ans correspond à environ 11 470 années solaires. Le dernier maximum glaciaire, établi à 18 000 ans 14C BP (Before Present = 1950 A.D.), remonte ainsi en réalité à environ 21 000 ans avant l'actuel (i.e. 1950 de notre ère). L'étalonnage des dates 14C en années solaires est donc primordial pour établir l'âge réel des objets datés, la durée réelle des événements, et les taux de changement dans le temps. La différence diminue pour des âges plus récents. Même avec un facteur de correction aussi grand que 10% (ce qui n'est pas le cas), le suaire de Turin ne pourraît être vieilli de ...700 ans ! (voir plus bas).
La croyance populaire est à l'effet qu'on puisse dater n'importe quoi avec le 14C. Il faut bien voir, et c'est très important, que cette méthode ne s'applique qu'aux matériaux qui ont déjà été vivants, comme du bois, des coquilles, du lin, etc. Inutile de penser dater des outils de métal ou des pointes de flèches en silex (SiO2) avec cette méthode.
Il y a une autre limitation très importante à la méthode : le temps impliqué. Avec les méthodes de l'uranium-plomb, du rubidium-strontium ou même du potassium-argon (voir plus-haut), la demie-vie s'exprime en milliards d'années. Avec le 14C, on parle d'une demie-vie de 5730 ans. Le schéma qui suit montre l'implication d'une demie-vie aussi courte.

Au temps 0, on a 100% de 14C (barre rose). Après 5730 ans (la demie-vie de la désintégration), la moitié du 14C est désintégrée. Après un autre 5730 ans (11,460 ans au total), la moitié de la moitié est désintégrée; il reste le quart du 14C originel. Après un autre 5730 ans, il en reste 1/8, ... et ainsi de suite. Après 74,490 ans, il reste 1/8192 (= 0,000122) du 14C originelle. C'est peu, d'autant plus qu'au départ, la quantité de 14C par rapport au 12C était déjà faible. Analyser une si faible quantité devient très difficile. En pratique donc, le 14C est utile pour dater des objets qui ne sont pas plus vieux que 75 000 ans. On parle ici non plus en milliards, ni même en millions d'années, mais bien en quelques dizaines de milliers d'années seulement.
Le 14C est une méthode très utile en archéologie et en histoire. Elle a été utile pour clore certains débats: le suaire de Turin qui aurait servi à ensevelir le corps du Christ a été daté en 1988, par trois équipes indépendantes, dans une fourchette d'âge entre 1260 et 1390 ans, donc un suaire fabriqué au Moyen-Âge. Le bois du soi-disant trône de St-Pierre a aussi été daté du Moyen-Age.
La méthode est aussi utilisée en géologie des dépôts superficiels qui souvent sont plus jeunes que la limite de 75 000 ans. Les dépôts de la Mer de Champlain, par exemple, sont datés au 14C, en utilisant les coquilles et le bois fossile de ces dépôts. Après étalonnage, ces dates 14C permettent d'établir que la Mer de Champlain s'est mise en place il y a 13 100 ans environ, et qu'elle a pris fin il y a 10 600 ans environ avant l'actuel. Elle aura donc duré environ 2500 années solaires (mais seulement 1700 années radiométriques au 14C; voir plus haut).
 | Retour au plan 4.1 |  |